Disputationsvortrag: Einleitung

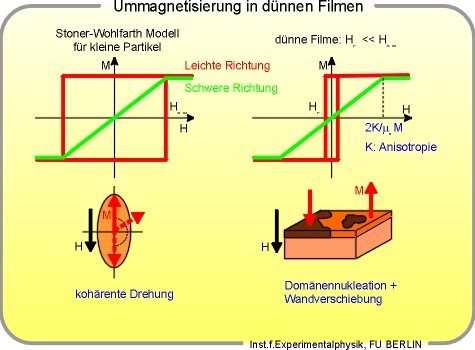
Hierzu möchte ich ein einfaches Modell zur Ummagnetisierung für kleine Partikel, das sogenannte Stoner-Wohlfarth-Modell, in Erinnerung rufen. Dabei betrachtet man ein uniachsiales System, bei dem ohne äußeres Magnetfeld die Magnetisierung eindomänig entlang der sogenannten leichten Richtung vorliegt. Legt man nun ein äußeres Feld H an, so bedarf es einer Feldstärke H_SW, um den Film durch kohärente Drehung der magnetischen Monente umzumagnetisieren. Es ergibt sich die dargestellte rechteckige Form für eine leichte Magnetisierungsrichtung. Liegt das äußere Feld jedoch senkrecht zu einer leichten Magnetisierungsrichtung, so folgt eine lineare Magnetisierungskurve. Im Stoner-Wohlfarth-Modell erhält man als Feld H_SW, bei den die Magnetisierung in Richtung des äußeren Feldes liegt, für leichte und schwere Richtungen denselben Wert.
Ein derartiges Verhalten wird im Bereich dünner Filme jedoch nicht gefunden. Es hat sich gezeigt, daß die Koerzitivfeldstärke H_C - also die Feldstärke, die zum Ummagnetisieren entlang einer leichten Richtung nötig ist - wesentlich kleiner ist als die Sättigungsfeldstärke bei Magnetisierung entlang einer schweren Richtung. Dieses Verhalten ergibt sich daraus, daß es bei dünnen Filmen bei bereits geringerer Feldstärke zur Nukleation von magnetischen Domänen mit entgegengestzter Magnetisierungsrichtung kommt. Da diese Domänen energetisch günstiger sind, wachsen sie durch Domänenwandverschiebung rasch an.
Das Maß für den Energieunterschied zwischen leichter und schwerer Magnetisierungsrichtung ist die Anisotropie K. Ist sie im Stoner-Wohlfarth-Modell proportional zur Ummagnetisierungsfeldstärke, so gilt dies für dünne Filme nicht.
Mit diesen Modellvorstellung können einfache Hysterese-Formen erklärt werden, jedoch können keine Aussagen darüber getroffen werden, ob der Ummagnetisierungsprozeß durch die Domänennukleation oder Wandverschiebung beherrscht wird. Zudem können Hysterse-Kurven mit von den beiden Extremfällen abweichenden Formen nicht erklärt werden.

Hierfür bedarf es magnetisch abbildender Methoden ...

	Blättern:
Überblick			4. Seite