
steigt die Remanenzmagnetisierung mit zunehmender Schichtdicke rasch an.
Zur Erinnerung ist das STM-Bild für 1.9 ML hier noch einmal klein wiedergegeben.
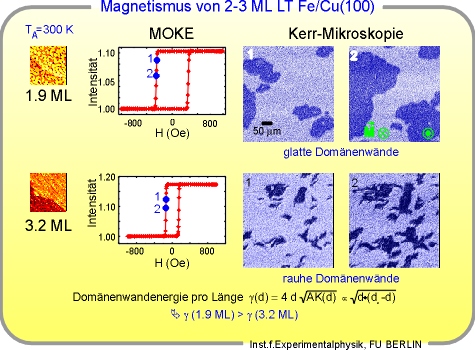
Mit polarem MOKE mißt man eine rechteckige Hysterese-Kurve. Im Gegensatz zu 0.9
ML ist der Film deutlich homogener und bewirkt, daß Koerzitivfeld und
Sättigungsfeld zusammenfallen. Die Ummagnetisierung erfolgt nach dem Schema, wie
ich es zu Beginn des Vortrages dargestellt habe: Kerr-Mikroskop-Aufnahmen
belegen, daß es zur Nukleation von Domänen mit entgegengesetzter
Magnetisierungrichtung kommt. So weist beispielsweise in den dunklen Bereichen
die Magnetisierung in die Filmebene hinein, in den hellen Bereichen zeigt sie
aus ihr heraus. Die eigentlich Ummagnetisierung erfolgt dann durch Verschiebung
der Domänenwände bei nahezu unverändertem äußeren Feld. Gezeigt ist jeweils ein
Ausschnitt von etwa 500 x 500 mm².
Bei größerer Fe-Bedeckung nimmt die Koerzitivfeldstärke ab (von 315 Oe bei 1.9 ML
auf 150 Oe bei 3.2 ML). Die Ummagnetisierung erfolgt wieder durch Nukleation
entgegengesetzt magnetisierter Domänen und ihrem anschließenden Wachstum,
jedoch ist die Form der Domänenwände im Fall von 3.2 ML deutlich rauher als bei
1.9 ML.
Wie kann man das verstehen?
Nun, hierfür muß man die Energie berechnen, die zum Ausbilden einer Domänenwand
benötigt wird. Da die Schichtdicke d in jedem der beiden Fälle konstant ist, muß
man die Domänenwandenergie pro Einheitslänge für 1.9 ML und 3.2 ML bestimmen.
Nach einer Standardabschätzung ist sie in cgs-Einheiten gleich 4 mal
Schichtdicke mal der Wurzel aus dem Produkt von Austauschintegral A und
effektiver Anisotropie K. Berücksichtigt man die Dickenabhängigkeit der
Anisotropie, so ergibt sich diese Proportionalität. Ohne hierauf näher eingehen
zu wollen, kann man jedoch feststellen, daß die Domänenwandenergie mit steigender
Schichtdicke bis hin zur Reorientierungsschichtdicke abnimmt. Dies kann auch
damit plausibel gemacht werden, daß die Anisotropie 2. Ordnung für die
Spin-Reorientierung bei 3.8 ML verschwindet und folglich die Anisotropie
bei 3.2 ML kleiner als bei 1.9 ML ist.
Somit ergibt sich, daß die Wandenergie bei 1.9 ML größer ist als bei 3.2 ML.
Dies hat im konkreten Fall zur Folge, daß die bei beiden Filmen vorhandenen
Substratdefekte bei 3.2 ML zu einer Wanddeformation führen, während sie wegen
der höheren Wandenergie bei 1.9 ML überwunden werden, da es hier energetisch
günstiger ist, die Defektbereiche umzumagnetisieren, um die Wand möglichst
kurz zu lassen.
Ich kome nun zur Spin-Reorientierung ...
| Blättern: | |||
| 12. Seite | 14. Seite | ||