
Im folgenden werde ich über Ergebnisse berichten, die zum Teil noch
aus meiner Doktorarbeit stammen, in der ich eine Aperatur für
UHV-Kerr-Mikroskopie mit kombiniertem STM und
magneto-optischem Kerr-Effekt (MOKE) aufgebaut habe.
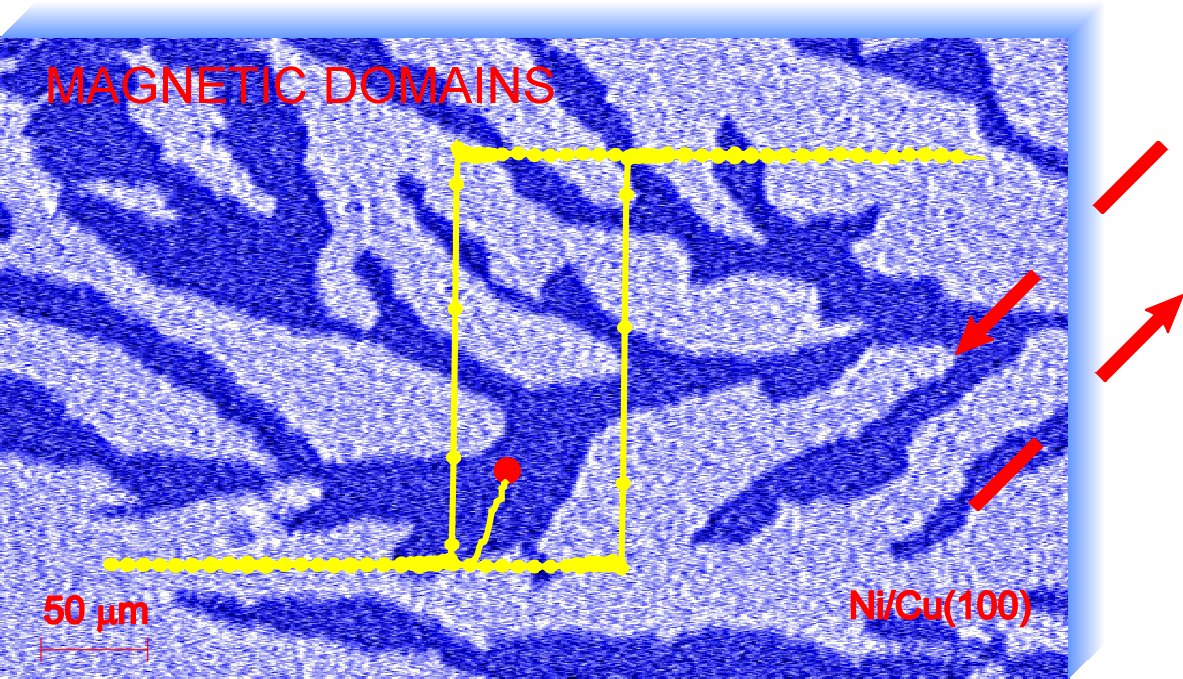
Dieses Beispiel hier zeigt ein Multidomänen-Bild, das während des
Ummagnetisierens mittels Kerr-Mikroskopie aufgenommen
wurde. Die entsprechende Hysterese-Kurve ist hier gelb eingezeichnet.
Aus Platzgründen verzichte ich hier auf die
experimentelle Beschreibung. Die folgenden
dynamischen Messungen der Ummagnetisierung sind von grundlegender Bedeutung
im Bereich magnetischer Speichertechnologie.
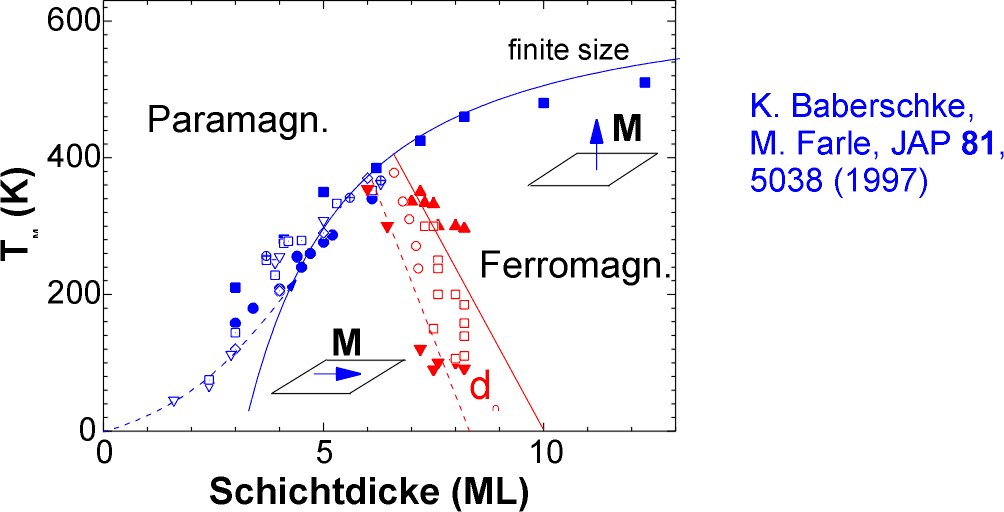
Die magnetischer Eigenschaften des Systemes Ni/Cu(100) sind in dieser
Auftragung kurz zusammengefaßt, die ich aus einer
Veröffentlichung von Baberschke und Farle gestohlen habe. Bei
Raumtemperatur liegt die leichte Magnetisierungsrichtung bis zu
etwa 7 ML in der Filmebene und klappt dann wegen der magneto-elastischen
Anisotropie aus der Filmebene heraus. Diese
senkrechte Anisotropie bleibt bis zu einer Schichtdicke von etwa 30 ML
erhalten. Erst bei dieser Schichtdicke relaxiert der Film
und die Formanisotropie zwingt die leichte Richtung in die Filmebene.
Im folgenden beschränke ich mich auf das Ummagnetisierungsverhalten
bei etwa 15 ML, also im technologisch besonders
interessanten Bereich senkrechter Magnetisierung.

Folglich mißt man mit polarem magneto-optischen Kerr-Effekt, also
bei senkrechtem äußerem Magnetfeld, rechteckige
Hysterese-Kurven mit 100%iger Remanenz. Bei 15 ML liegt die
Koerzitivfeldstärke, also die halbe Breite der Hysterese-Kurve
bei etwa 12.5 Oe. Bei der Aufnahme von Hysterese-Kurven wird
bekannterweise die Magnetisierung in Abhängigkeit vom
äußeren Magnetfeld gemessen, Hierfür wird jeweils das
äußere Feld H eigestellt und nach einer festvorgegebenen Zeit das
MOKE-Signal, welches proportional zu M ist, gemessen. Insofern handelt
es sich also um eine statische Messung.
Bei dynamischen Messungen hingegen wird die Zeitabhängigkeit der
Magnetisierung gemessen, also für jeweils ein
festvorgegebenes Magnetfeld die Magnetisierung in Abhängigkeit von
der Zeit gemessen. Hierfür wird zuerst ein Startfeld H1
eingestellt, um die Probe remanent in eine Richtung zu sättigen.
Zum Zeitpunkt t=0 erfolgt die Ummagnetisierung mit einem
Gegenfeld H2, welches üblicherweise kleiner als das Koerzitivfeld
ist. Man stellt fest, daß bereits geringere Felder als HC
ausreichen, um die Probe in endlicher Zeit nahezu vollständig
umzumagnetisieren.
Nach einem klassischen Modell von Fatuzzo, das bis heute seine
Gültigkeit immer wieder gezeigt hat, erwartet man bei einer
Ummagnetisierung, die durch Nukleation vieler entgegengesetzt
magnetisierter Domänen und ihrem anschließenden Wachstum
durch Wandverschiebung bestimmt wird, eine exponentielle
Zeitabhängigkeit der Magnetisierung. Die Ummagnetisierungszeit t
wiederum hängt von der Aktivierungsenergie EA eines
Barkhausen-Sprunges mit dem Volumen VB und dem entsprenden
äußerene Feld H2 ab.
Im vorliegenden Fall erhalten wir jedoch eine Ummagnetisierungskurve, die
eindeutig nicht exponentiell abfällt. Die Form der
Kurven ist dabei jeweils identisch. Es ergeben sich aus diesen Messungen
zwei Fragestellungen:
1. Woher kommt der „Buckel“?
2. Wieso kein exponentieller Abfall?

Darüberhinaus ergibt sich eine weitere Überraschung, wenn man das
Startfeld H1 variiert. Bei den eben gezeigten Kurven war
das Startfeld zur Sättigung der Magnetisierung 40 mal so groß wie
das statische Koerzitivfeld HC. Dann bewirkt ein Gegenfeld
H2 von 60% des Koerzitivfeldes keine sofortige Ummagnetisierung.
Beträgt das Startfeld jedoch nur das 1.4-fache von HC, so
erwartet man nach den MOKE-Messungen ebenfalls eine vollständig
gesättigte Probe, mißt jedoch beim gleich großen
Gegenfeld bereits eine sekundenschnelle Ummagnetisierung. Dieses
Verhalten ist unerklärlich, da die Ummagnetisierungszeit
nicht vom Startfeld sondern nur vom Gegenfeld abhängt.
Zudem sieht man hier deutlich einen exponentielle Abhängigkeit
der Magnetisierung von der Zeit. Es ergibt sich also die Frage:
Was ist hier anders?
Um diese Frage beantworten zu können, muß man Einzelheiten über den Ummagnetisierungsprozeß kennen. Hierfür haben wir an derselben Probe ortsaufgelöste Ummagnetisierungsmessungen mit Hilfe des in-situ verfügbaren Kerr-Mikroskopes durchgeführt.

Auch diese Messungen sind in polarer Geometrie enstanden, so daß sich ein
Domänenkontrast von hell und dunkel für in die und
aus der Filmebene heraus magnetisierte Bereiche ergibt. Die Ummagnetisierung
erfolgt im wesentlichen durch Verschiebung
einer einzelnen Domänenwand. Diese Wand wird an verschiedenen
Substratdefekten gepinnt. Die Vorzugsrichtung der
Domänenwand entspricht den {110}-Richtungen des Ni-Filmes. Hierbei
handelt es sich um die leichte Richtung bei in-plane
magnetisierten Filmen. Da innerhalb der Domänenwand die Magnetisierung
durch die Filmebene dreht, stellt sich als
Wandrichtung die innerhalb der Ebene bevorzugte Richtung ein.
Die Wand verschiebt sich bei nahezu konstanten Feld über das
Gesichtsfeld des Mikroskopes, bis bei einem Gegenfeld von etwa
der Koerzitivfeldstärke offensichtlich der gesamte Film ummagnetisiert
ist. Vor Aufnahme dieser Bilder wurde der Film mit
einem Startfeld vom 40fachen des Koerzitivfeldes gesättigt.
Magnetisiert an die Probe jedoch ausgehend von diesem Bild wieder
zurück, so ergibt sich ein völlig anderes Bild...

Bereits bei wesentlich kleineren Feldern H2 „reißt“ der vorher
scheinbar eindomänige Zustand auf. Diese Risse werden rasch
breiter, bis sich wieder die charakteristischen
Domänenwand-Vorzugsrichtungen ausbilden.
Was ist die Ursache für dieses erstaunliche Verhalten? Eine
genaue Untersuchung ergibt, das die Startpunkte dieser „Risse“ oder
„Kanäle“ jedes Mal wieder dieselben sind und mit Pinningcentern
bei der Ummagnetisierung übereinstimmen. Diese
Pinningcenter verhindern die Weiterbewegung der Domänenwand.
Unser mikroskopisches Verständnis ist auf der nächsten Folie
skizziert...

In dem Modell verschiebt sich eine einzelne Domänenwand von links nach
rechts. Die Wand trennt Bereiche, die
entgegengesetzt magnetisiert sind. An einem Substratdefekt wird die Wand an
ihrer Ausbreitung gehindert (gepinnt). Seitlich des
Defektes schreitet die Domänenwand voran. Da die entgegengesetzte
Magnetisierungsrichtung energetisch günstiger ist, sollte
sich die Wand hinter dem Defekt wieder schließen. Genau dies kann
jedoch nicht passieren, da sich die doppelte Domänenwand
nicht auflösen kann. Innerhalb jeder Bloch-Wand dreht die Magnetisierung
durch die Filmebene hindurch. Da die Doppelwand
durch Pinning enstanden ist, ergibt sich eine vollständige 360o-Drehung
der Magnetisierung.
Die Breite dieser Struktur muß dabei unter der Auflösung des
Mikroskopes von 2 mm liegen, da die Kanäle sonst direkt in der
Ummagnetisierungsserie gesehen werden würden. Erhöht man das
äußere Feld hinreichend (z.B. auf 40 mal HC), so löst sich die
Doppelwand vermutlich durch Überwindung des Pinningcenters von hinter auf.
Im anderen Fall sind die gefangenen Domänenwände noch vorhanden und
bei Anlegen eines kleinen Gegenfeldes liegen bereits
Bereiche mit entgegengesetzter Magnetisierung vor, also Kanal-artige
Nukleation. Diese sind energetisch günstiger und breiten
sich aus, was zu einer Verbreiterung der Kanäle führt. Dadurch
sind sie im Kerr-Mikroskop zu sehen.
Als erstes Ergebnis können wir also festhalten, daß wir im Fall
eines kleinen Startfeldes eine nahezu instantane
Ummagnetisierung mit exponentiellem Abfall beobachten, da viele
Nukleationskeine vorliegen und somit die Voraussetzungen
für das Fatuzzo-Modell gegeben sind.
Auch das Verhalten bei großem Startfeld ist nun verständlich...

Die Ummagnetisierung erfolgt durch Nukleation einer oder weniger Domänen
und anschließender Wandverschiebung. Dabei
liegt der Nukleationskeim außerhalb des Gesichtsfeldes von MOKE und
Kerr-Mikroskopie. Bei konstante Wandgeschwindigkeit
und rundem Gesichtsfeld ergibt sich die gezeigte theoretische
Ummagnetisierungskurve, die qualitativ sehr schön mit der
gemessenen übereinstimmt.
Die Nukleation erfolgt jeweils an derselben Position. Die Geschwindigkeit
der Wandverschiebung bestimmt die
Ummagnetisierungszeit t, die wiederum exponentiell vom Gegenfeld H2
abhängt. In logarithmischer Auftragung erkennt man
sehr schön die Übereinstimmung zwischen Experiment und Theorie in
der abfallenden Geraden. Aus der Steigung dieser
Geraden kann man das mittlere Volumen jedes elementaren Barkhausen-Sprunges
berechnen. Oder, bei Annahme eines
quadratischen Ummagnetisierungsbereiches, eine Barkhausen-Länge
von etwa 270 nm.
Ein Vergleich mit der Morphologie dieser Filme legt einen Schluß
für die Ursache dieser Barkhausen-Länge nahe...

Die Topographie der Ni-Filme ist sehr rauh mit Strukturgrößen von wenigen 10 nm. Dagegen liegt die Stufenbreite des Cu(100)- Substrates mit mehreren hundert nm genau in der Größenordnung der berechneten Barkhausen-Länge. Ein Fit der Abfallkonstanten der Magnetisierungskurve bei kleinem Startfeld (exponentieller Abfall) ermöglicht bei Kenntnis des Barkhausen-Volumens die Bestimmung der Aktivierungsenergie. Sie liegt im Bereich von einem eV und beträgt somit einige Prozent der Domänenwandenergie einer Wand der Barkhausen-Länge. Da die Domänenwandenergie linear mit der Schichtdicke ansteigt, erscheint es plausibel, daß ein Hemmnis jeden Barkhausen-Sprung durch veränderte Schichtdicken an Substratstufen hervorgerufen wird.