Sfb290
TP A2 UP II: ac-susceptibility in UHV
(C. Rüdt,
K. Baberschke)
Mutual Inductance (MI) and the Magneto-Optical Kerr-Effect (MOKE) in
an ac mode are used to measure the magnetic differential susceptibility
of ultrathin single films, bi- and trilayers. The critical temperatures
for the onset of a spontaneous magnetization parallel and perpendicular
to the film plane are measured. Moreover, the critical exponent gamma
as well as the higher harmonics of the ac susceptibility can be determined
via MI measurements close to TC.
- The para-/ferromagnetic phase transition in Ni(001) films on Cu(001)
-
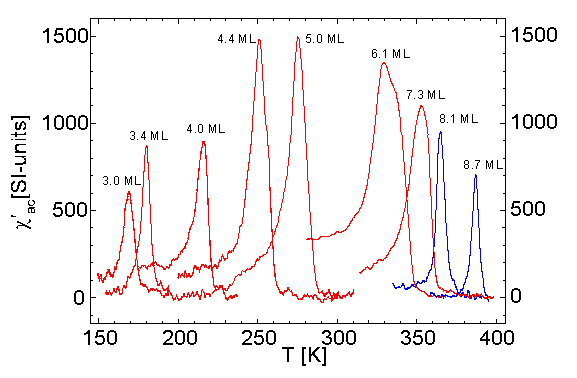
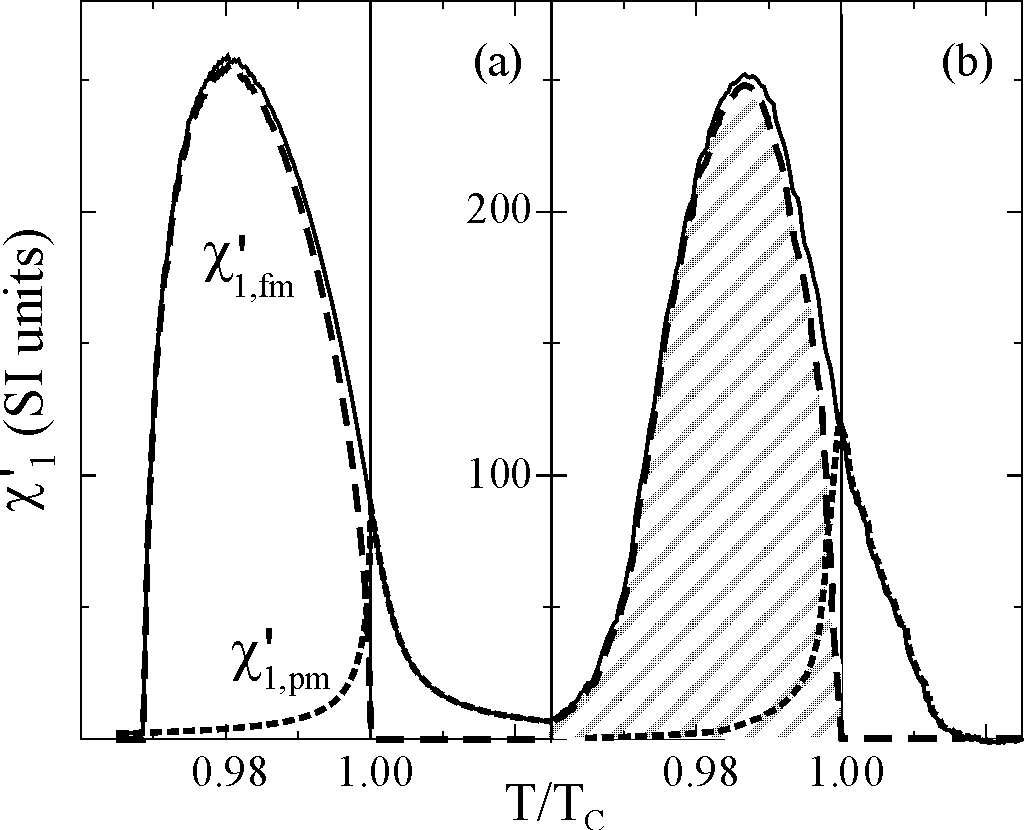
For in plane magnetized films the susceptibility peak
shows up at the Curie temperature TC as given by the Curie-Weiss
law (Fig. 1). Note the monolayer sensitivity and the absolute calibration
of our UHV compatible setup.
- The influence of interlayer exchange coupling on the para-/ferromagnetic phase transition in magnetic trilayers
-
The ac susceptibility technique was used to investigate the
problem of ordering temperatures in magnetic trilayers. Single ultrathin
magnetic layers have a TC where the internal susceptibility
chiint diverges and the experimentally measured susceptibility
chiexp shows large values as Fig. 1 reveals. Now a question
arises when one prepares a trilayer, i.e. two single magnetic layers
like Co and Ni separated by a non-ferromagnetic spacer such as Cu. Will
the interlayer exchange coupled system Co/Cu/Ni show one or two Curie
temperatures? In Fig. 2(a) the dotted line depicts chi exp for
a 5 ML /Ni/Cu(001) capped by 25 ML of Cu. The maximum is at about TC.
The solid line represents chiexp after the evaporation
of 2 ML Co on the top of the Cu/Ni bilayer. One sees a very large signal
at about 430 K where is the TC of Co and a small one at about
250 K where is the TC of the Ni layer [Ref. 206] . Two susceptibility
peaks were recorded only for trilayers with very weak coupling. Jinter
acting as a field it suppresses chiexp below the experimental
sensitivity and shifts it to higher temperatures as the calculations
of Fig. 2(b) carried out by P.J. Jensen/K.H. Bennemann (Sfb290, TPA1)
[Ref. 229] and more recent
experiments [Ref. 215]
reveal. The shift DeltaT of the ordering temperature of Ni in the presence
of Jinter was shown by x-ray magnetic circular dichroism (XMCD)
experiments to be always positive and to present an oscillatory character
following the periodicity of Jinter [Ref. 212] . DeltaT was found
to be as large as 90 K when one decreases the Ni layer thickness to about
3 ML. This effect can be only understood in terms of the reduced dimensionality
of the ferromagnetic layers and can not be reproduced by the conventional
Molecular Field Theory (MFT) which ignores spin fluctuations [see common
work with TPA1, Ref.
229] . Finally, the problem of phase transitions in coupled two-dimensional
ferromagnetic layers is dealt in [Ref. 252].
- Curie temperature and critical exponent gamma in magnetic superlattices
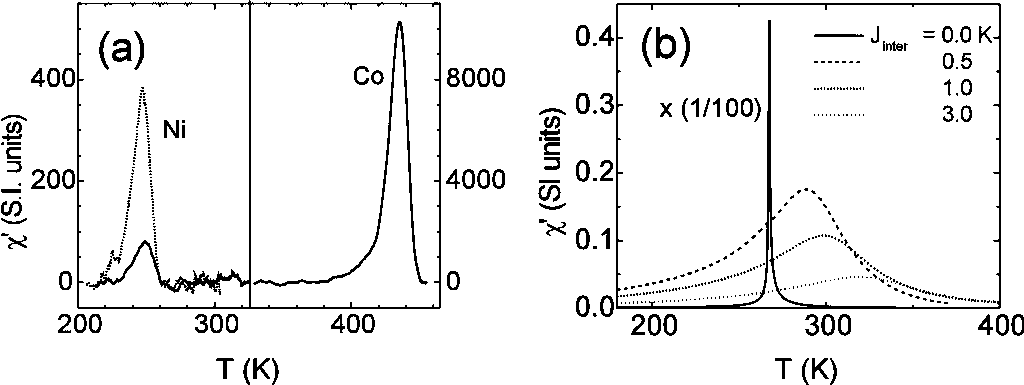 Fig. 2
Fig. 2
The problem of critical
phenomena in Fe2/V5 magnetic superlattices is
currently studied by ac susceptibility measurements. The high structural
and magnetic homogeneity of the samples [Ref. 193] results in very
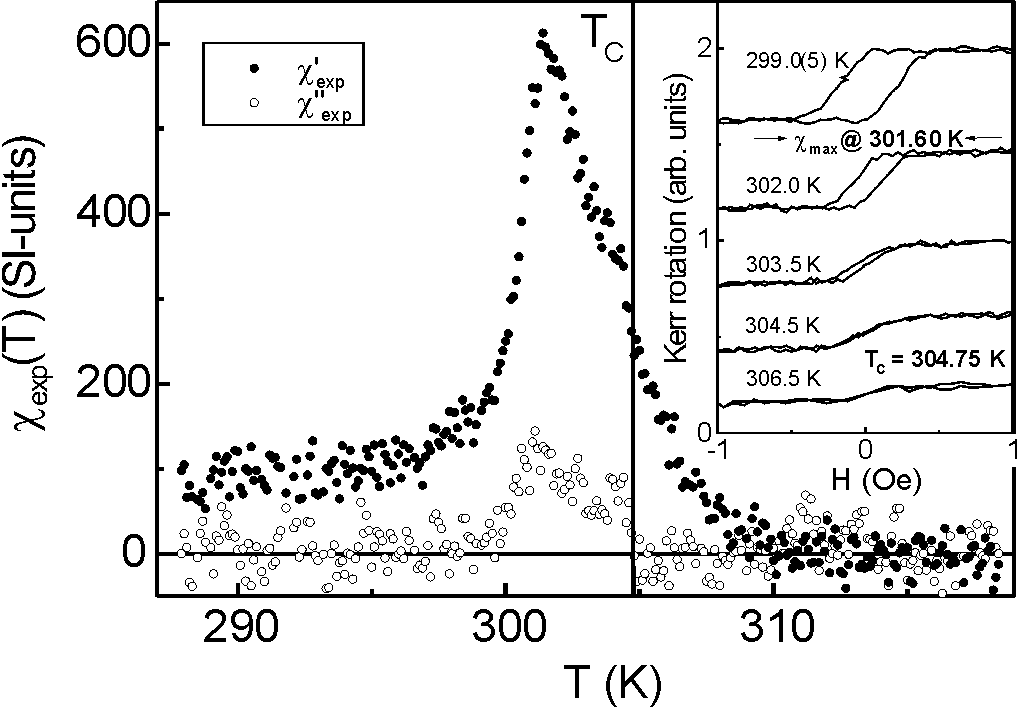
narrow chiexp peaks (» 3
K), see Fig. 3. The amplitude of the oscillatory field is as small as
17 mG and all static fields were compensated below 10 mG. Before attempting
any critical fitting one must determine independently TC.
In Fig. 3 with closed symbols we depict the dispersive chi'exp
and with open symbols the dissipative part, chi''exp, of chiexp
. It is well-known that in the ferromagnetic phase there are hysteresis
losses, while in the paramagnetic not. Thus, the correct TC
has to be placed at the onset of chi''exp (indicated by a vertical
solid line). Note that at the maximum of chi'exp up to 2-3
K above, there is significant hysteresis as the MOKE loops in the inset
of Fig. 3 reveal. Therefore, the maximum of chi'exp does not
correspond to T C [Ref. 243] . After determining
independently the TC one has to correct chi' exp
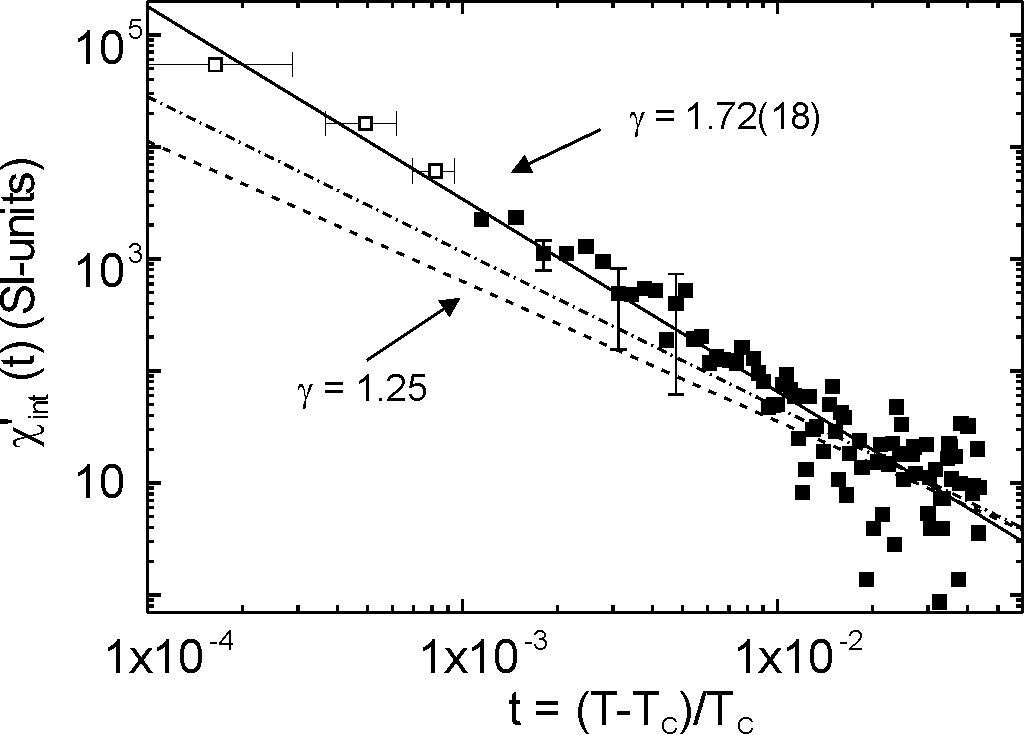
for the demagnetizing factor. Then, one may plot in a double logarithmic
diagram chi'int = chi+
0 t-gamma as a function of the reduced temperature
t, Fig. 4. By linear regression of the data down to t=10-4
one determines from the slope of the solid line the critical amplitude chi +0=0.024(3) and a critical exponent
gamma=1.72(10) consistent with the 2D-Ising model. A 3D-exponent (gamma=1.25,
dashed line) is clearly ruled out. Through the susceptibility analysis
we conclude that the reduced dimensionality of the Fe layers determine
the critical behavior at TC and Jinter should fade
away [Ref. 256] .
|
|
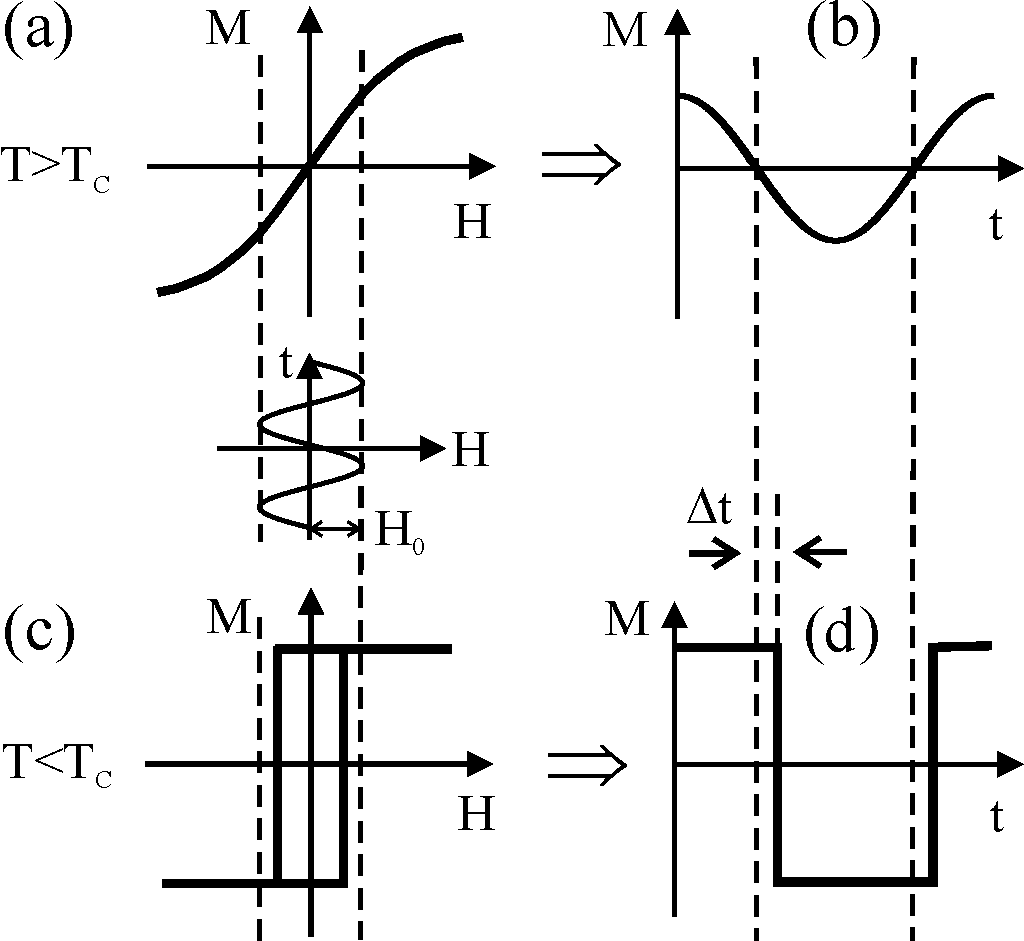
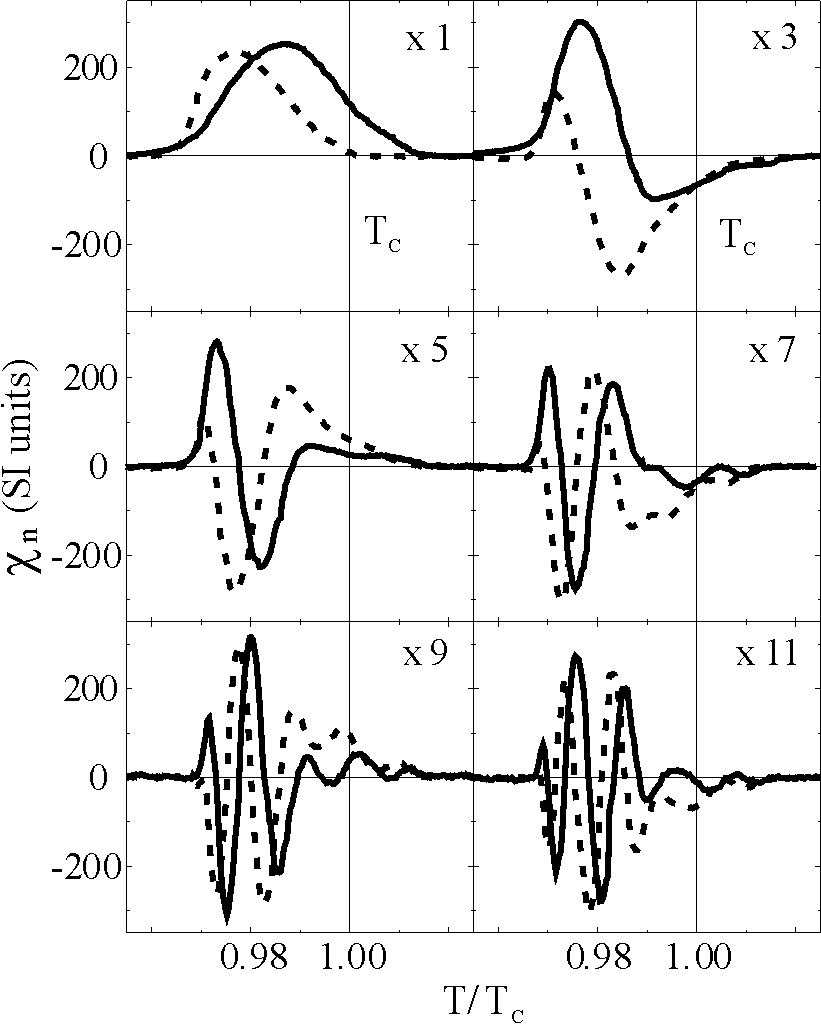
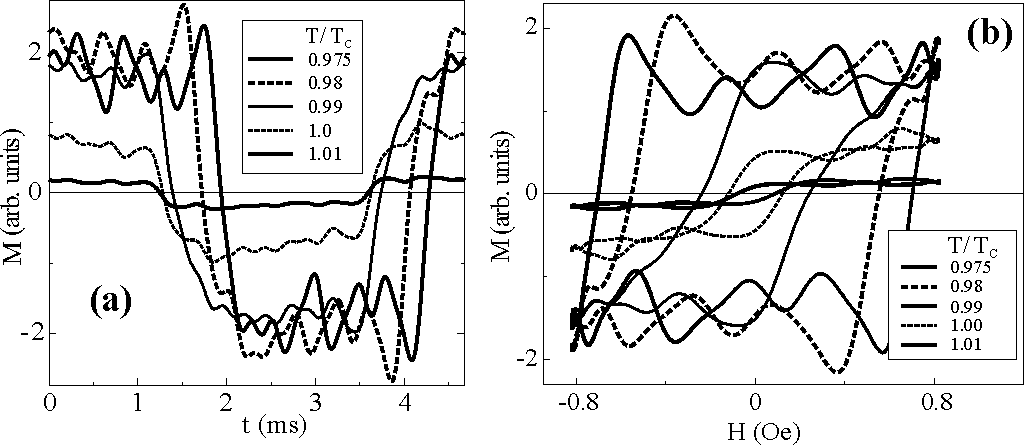
- Higher Harmonics of the ac susceptibility / Separation of para- and ferromagnetic contributions