FMR is one of the best techniques to determine the intrinsic magnetic anisotropy energy (MAE) quantitatively and with high precision. The temperature, angular and frequency dependent measurements in situ in UHV yield second- and fourth-order, in-plane and out-of-plane MAE constants as a function of temperature. All MAE constants are separated into interface and volume contributions K _i = K_i ^V +2K_i ^S/d   by investigations at different film thickness d and at constant reduced temperature t = T/T_C(d). Simultaneously the anisotropy of the orbital magnetic moment can be determined by the spectroscopic splitting factor, i. e. the g-tensor from the simple relation µ_L/µ_S = (g-2)/2 [Ref. 171, 210] . These experiments help to understand how these quantities are modified  in 3d and 4f films and sandwiches relative to the bulk. Extrapolation of the measured MAE constants to T=0K yields a direct comparison to first principles MAE calculations. In addition the magnetization dynamics and spin fluctuations on the nanosecond scale can be studied and the temperature dependence of the total magnetization of monolayers can be determined. Some highlights are given below.
 

• The anomalous spin reorientation transition in tetragonal Ni(001) films on Cu(001)

 

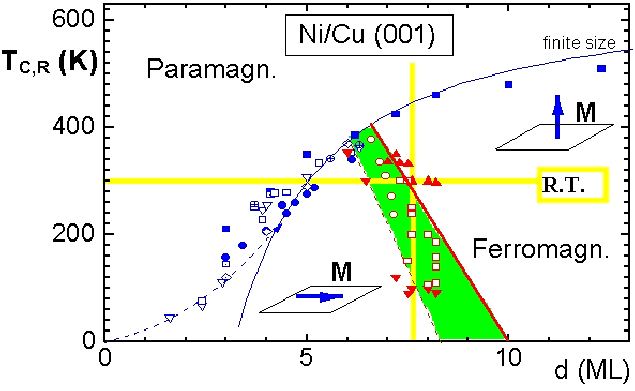
The magnetic phases in Ni/Cu(001) are shown as a function of temperature and film thickness d in Fig. 1 [Ref. 184] . The blue data points indicate the thickness dependent Curie temperature separating the paramagnetic and ferromagnetic phase. In the ferromagnetic region one finds a (T,d) parameter space with the easy axis of the spontaneous magnetization parallel and perpendicular to the film plane as indicated.

  Fig. 1

Both regions are separated by the green shaded space in which an equilibrium tilted magnetization is measured. Using the yellow lines as a guide one observes an anomalous reorientation from in-plane to out-of-plane with increasing thickness or temperature . This is opposite to the conventional observation in Fe and Co layers. The magnetization rotates as a function of temperature (fixed d) as well as a function of thickness (fixed T) continuously, indicating a second order transition.

Fig. 2

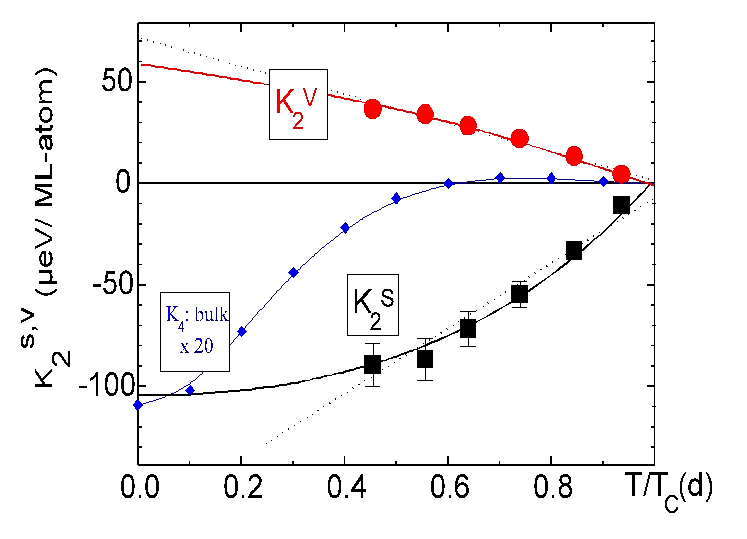
This unconventional reorientation is quantitatively understood by the measured temperature dependencies of interface and volume MAE  [Ref. 180,185] as shown in Fig. 2. K₂^V is positive favoring a perpendicular orientation while K₂ ^S is negative favoring an in-plane magnetization. Both decrease as a function of temperature. The different  temperature dependencies and the thickness dependent balance of shape anisotropy and intrinsic MAE explain the magnetic phase diagram of Fig.1 quantitatively.
 

 Fig. 3

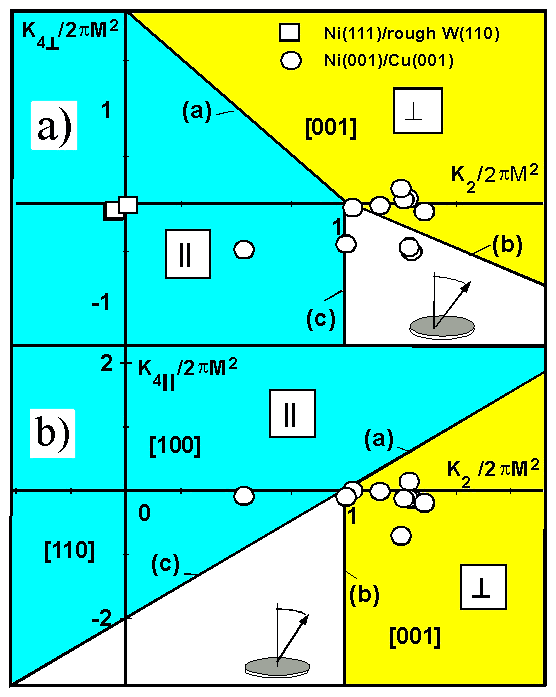
Fourth-order anisotropy constant must be included in the free energy density E to explain the tilted orientation (green area) in Fig.1 . In Fig. 3 (on the left) we show the threedimensional parameter set K _4|| = f(K₂) and K_4perp = f(K₂). All K_i are normalized to 2piM² [Ref. 176, 184] . The light blue (yellow) areas indicate an easy in-plane (perpendicular) spontaneous magnetization. The white region presents the parameter space for a tilted orientation.  The MAE constants vary as a function of film thickness and temperature. For different samples, temperatures and thicknesses the experimental data are indicated. As an example we show values for Ni/Cu(001) near the reorientation (green area in Fig.1) and for Ni(111)/W(110) [Ref. 120, 171] . Ni/W has very small K₄ and K₂ values (open squares), consequently this film has its easy axis in-plane under all conditions. Contrary Ni/Cu with large uniaxial K₂ values and moderate (negative and positive) K₄ values permits all orientations as an easy axis. The physical reason for this is the pseudomorphic growth and its tetragonal distortion, whereas Ni/W grows in an undistorted cubic phase.
 
 

• Magnetic anisotropy energy and spectroscopic g tensor in superlattices

 

 Fig. 4

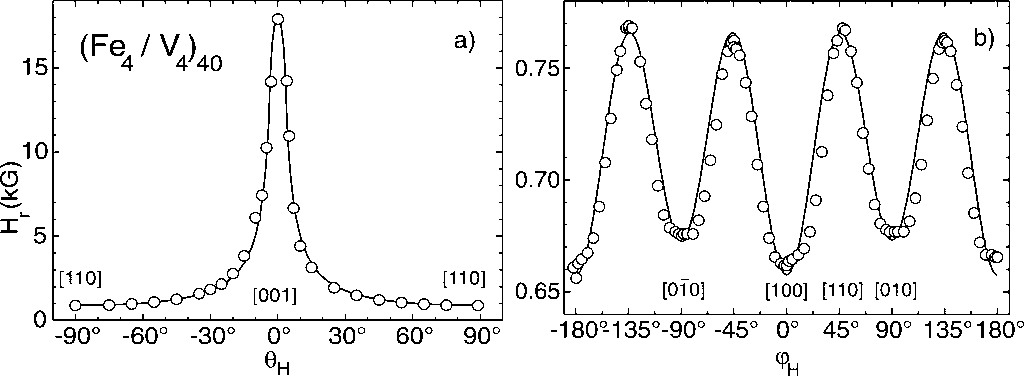
Recently we have employed FMR to measure the magnetic anisotropy constants and the spectroscopic g tensor of high quality single-crystalline Fe/V superlattices (SL) on MgO(001). The samples were provided from the Group of R. Waeppling, Uppsala University . FMR is the most suitable technique for determining all magnetic anisotropy constants via angular-dependent measurements [e.g. Refs. 184,193,235]. In Fig. 4 we show full polar- and azimuthal-angular-dependent FMR measurements of the resonance field H_r for an (Fe₄/V₄ )₄₀ SL on MgO(001). The indices 4 are MLs of Fe or V in one period, while 40 is the number of SL periods. From the positions of the H_r -minima at q_H= ±90^o , Fig. 4(a), we conclude that the magnetization lies in the film plane. In Fig. 4(b) we see a small in-plane anisotropy with minima along the [100] and [010] directions. In addition a smaller asymmetry between the two ideally identical [100] and [010] directions indicates the presence of a small step-induced anisotropy [Ref. 193] .
 

 Fig. 5

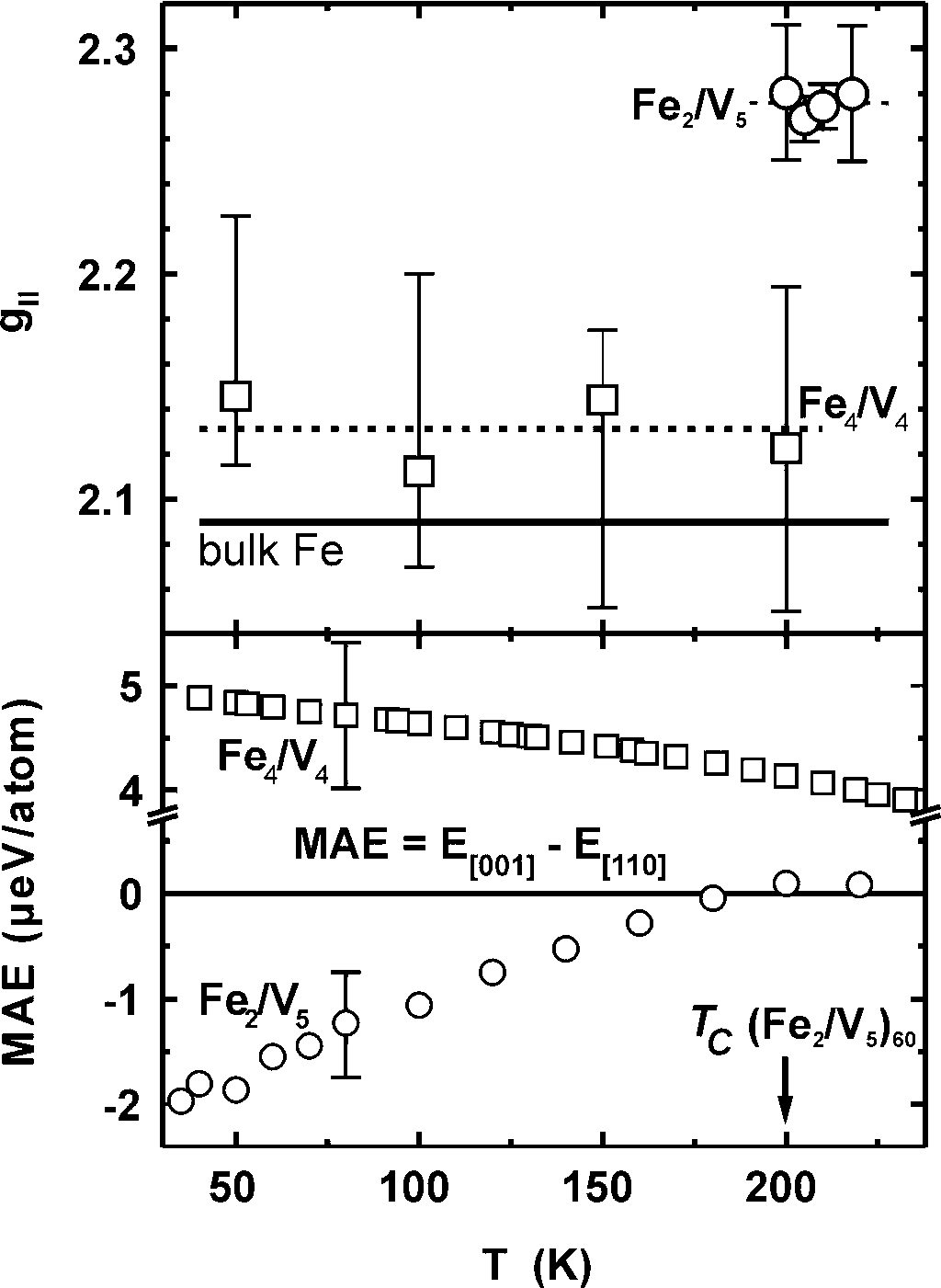
Frequency-dependent FMR measurements probe the components of the g tensor and through this the orbital magnetism through the equation: µ_L/µ_S = (g-2)/2 [Refs. 210, 234, 271] . FMR is the only technique that may provide independently values for the MAE and the anisotropy of the orbital moment (through measurements of the components of the g tensor). In Fig. 5(a) (on the left) we present the components g_// of the g tensor in the film plane for two Fe/V superlattices. The values of g_// are larger than the values of bulk Fe. Since g is a function of the magnetic moment it is temperature-independent. Note also that for the sample Fe₂/V₅ we probe g_// at temperatures higher than T_C as the magnetic moment persists above T_C. Unlike g_//, MAE is temperature-dependent. This is demonstrated in Fig. 5(b) for both Fe/V samples. For the Fe ₂/V₅ sample we may see that MAE vanishes at T_C .
 
 

• In situ FMR on magnetic trilayers: Direct determination of interlayer coupling
 
Another subject where FMR can give valuable information is the determination of interlayer exchange coupling J_inter in trilayers and multilayers. Recently we succeeded for the first time in a step-by-step in situ (in ultrahigh vacuum) investigation of J_inter via FMR in Ni/Cu/Co and Ni/Cu/Ni trilayers grown on Cu(001). In this process we first evaporate the one magnetic layer and the Cu spacer and measure the FMR signal (Fig. 6 bottom part, dotted lines). Then we evaporate the second magnetic layer. The FMR spectrum (Fig. 6 bottom part, solid lines) includes now two modes, the acoustic one where the two sublayer magnetizations precess in-phase, and the optic where they precess 180^o out-of-phase. From the position of the optic with respect to the acoustic mode we conclude that the coupling is antiferromagnetic-AFM for the Ni/Cu/Co and ferromagnetic-FM for the Ni/Cu/Ni trilayer. For better illustration, on the top of Fig. 6 we introduce calculated FMR spectra for various values of J_inter for the two cases of AFM and FM coupling and schematic diagrams of the two modes. The calculations also suggest an independent measure for J_inter provided the trilayer can be investigated before and after the deposition of the topmost ferromagnetic film, since it can be seen that the signal of the bottom film shifts due to the coupling to higher (AFM coupling) or lower (FM coupling) field values. Thus, analyzing this shift also yields J_inter in absolute units. For more details see [Ref. 244,272,273] .
 
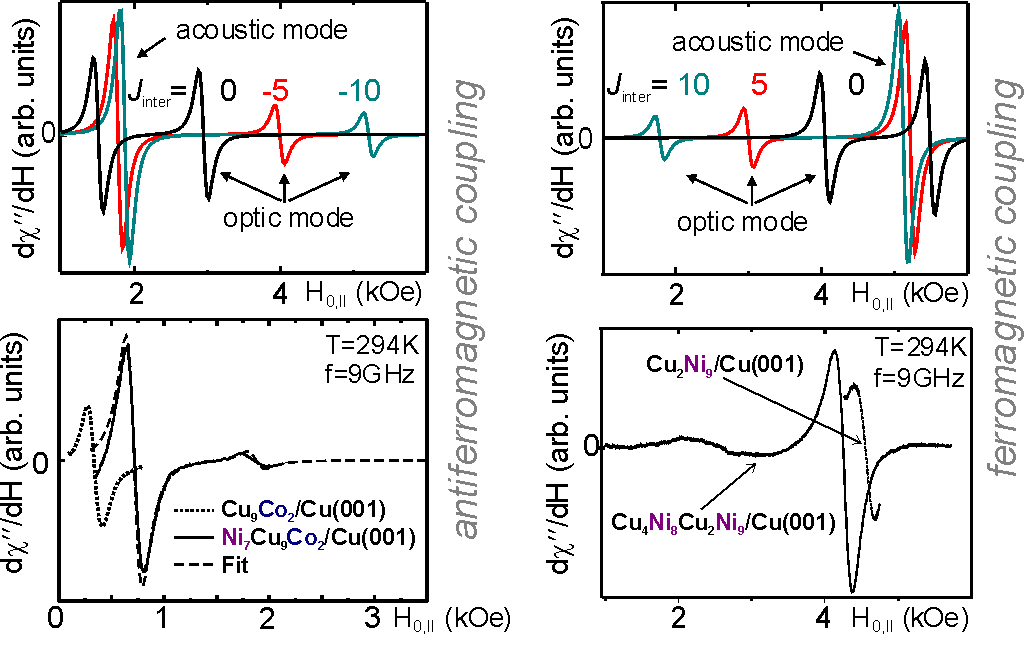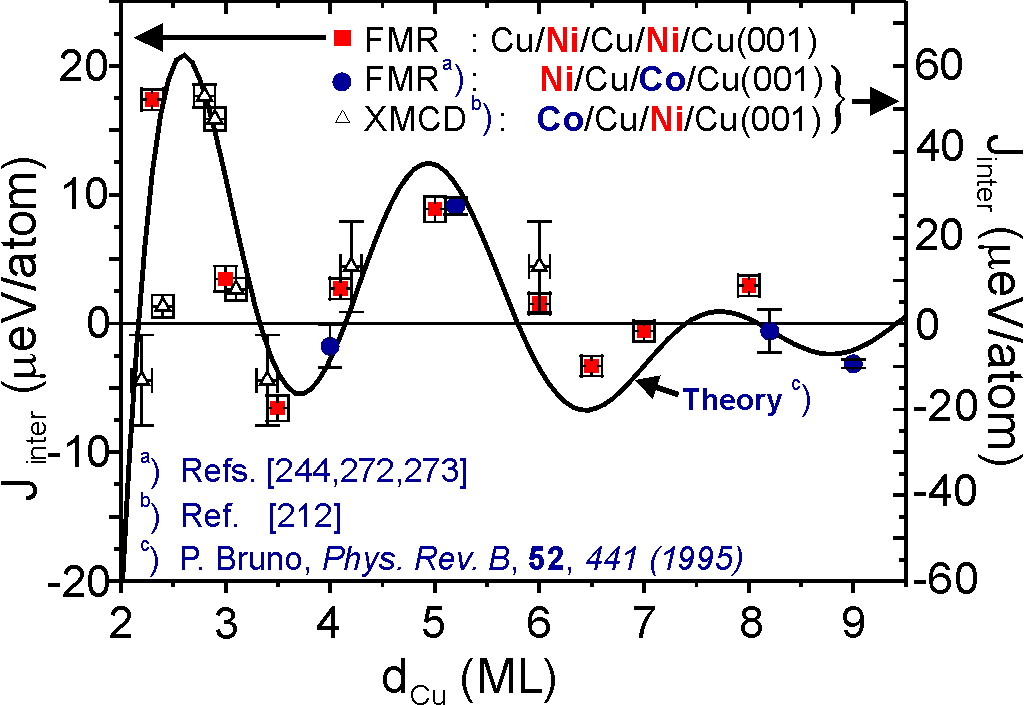
 Fig. 6

 
In Fig. 7 the coupling J_inter is plotted as function of spacer thickness d. The right y-axis refers to Ni/Cu/Co- (blue circles) the left y-axis to Cu/Ni/Cu/Ni-trilayers (red squares, Ref.[244,272,273]) and XMCD data of Co/Cu/Ni-trilayers (open triangles, Ref. [212]). Since XMCD is does not provide absolute units, the values were scaled on the y-axis accordingly. One observes a clear oscillatory behavior for both systems which is in accordance to existing theories (solid line). The in situ approach in particular has advantages for very small spacer thicknesses, since the growth conditions can be well controlled (Note that in Fig. 7 the spacer thicknesses range between 2-10 ML only, i.e. the small period of the oscillatory coupling can be observed). The possibility of FMR to yield absolute values for J_inter (note that positive values reflect ferromagnetic, negative ones antiferromagnetic coupling) allows to plot the y-axis in energy per particle. This enables one to compare the results in a direct way to ab initio calculations as it was done in Ref.[281].
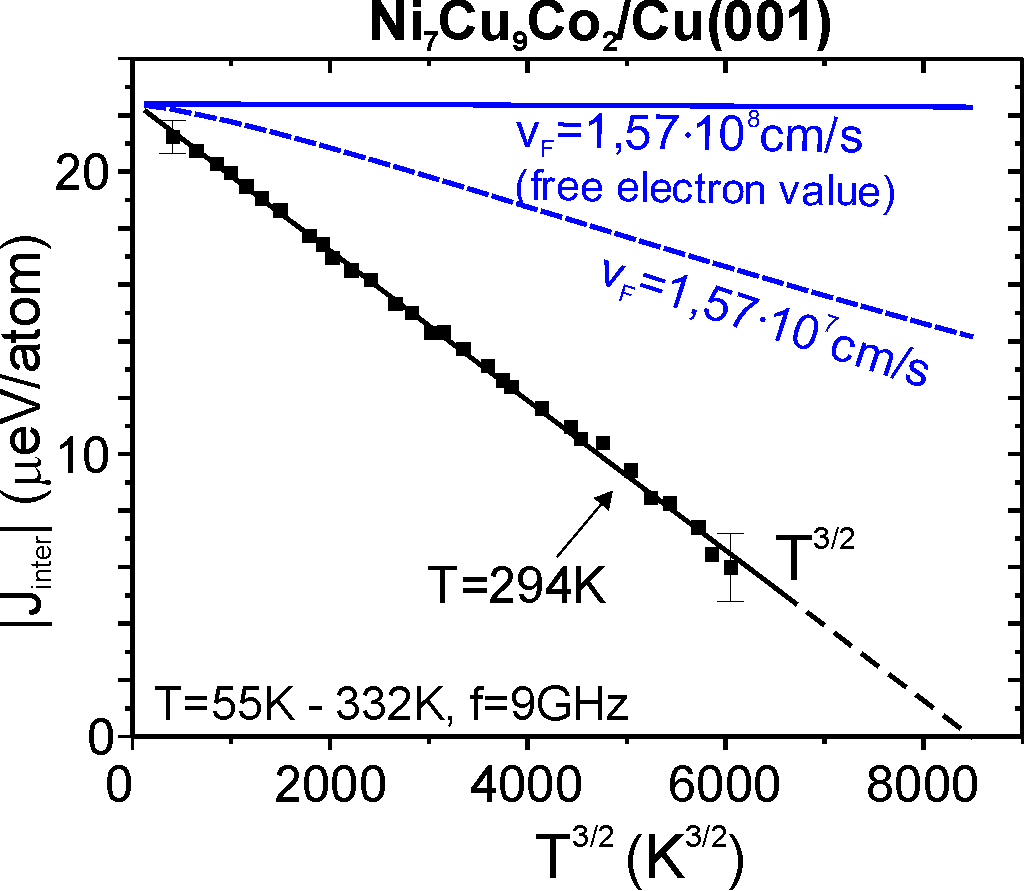
Another result is shown in Fig. 8 , where |J_inter| is analyzed as function of temperature T. Upon plotting the dependence as function of T ^3/2 a power law behavior is found within a wide temperature range. This confirms theoretical predictions that the temperature dependence of J_inter is governed by thermal spin waves created in the ferromagnetic layers (Ref. [267]). Models which take band structure effects in the spacer material as source of the reduction of the coupling (blue lines shown for different Fermi velocities of the spacer electrons) play a minor role (e. g. P. Bruno, Phys. Rev. B, 52, 441 (1995)).

Fig. 7

Fig. 8

 


• Magnetic Damping / Spin Dynamics
  

To control magnetization dynamics it is important to understand the microscopic damping of the magnetization vector. The magnetization dynamics can be studied by analysing the FMR linewidth which is directly related to the relaxation of the magnetization of the system. The most widely found inclusion of damping of the spin motion used in literature is the Gilbert approach given by the phenomenological expression

.

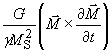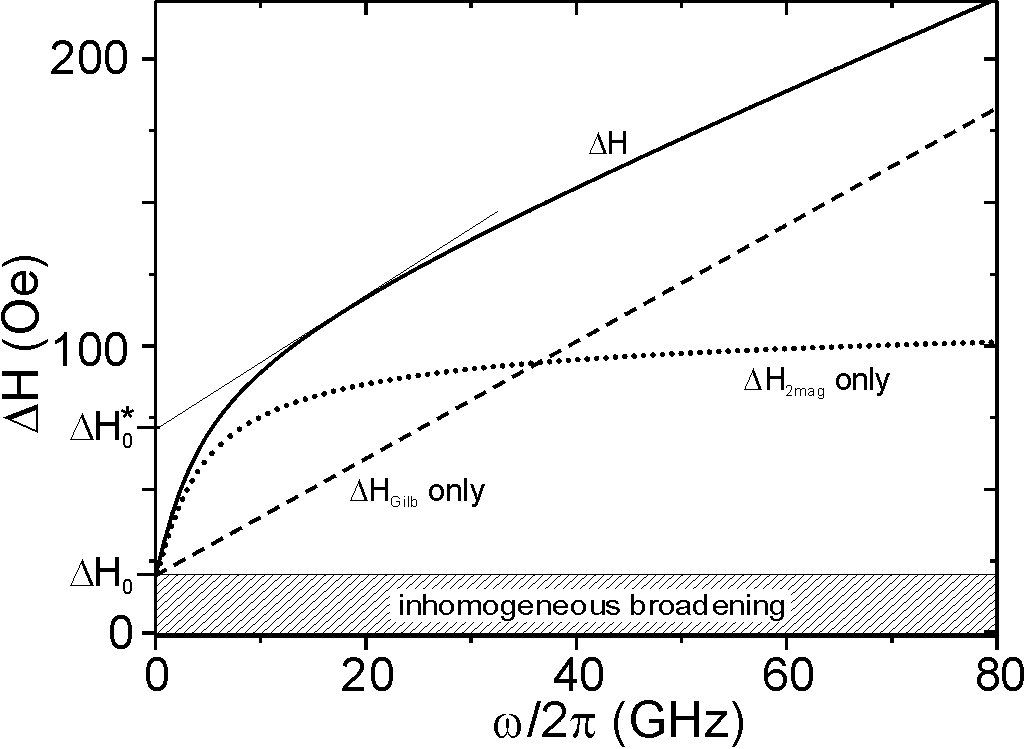
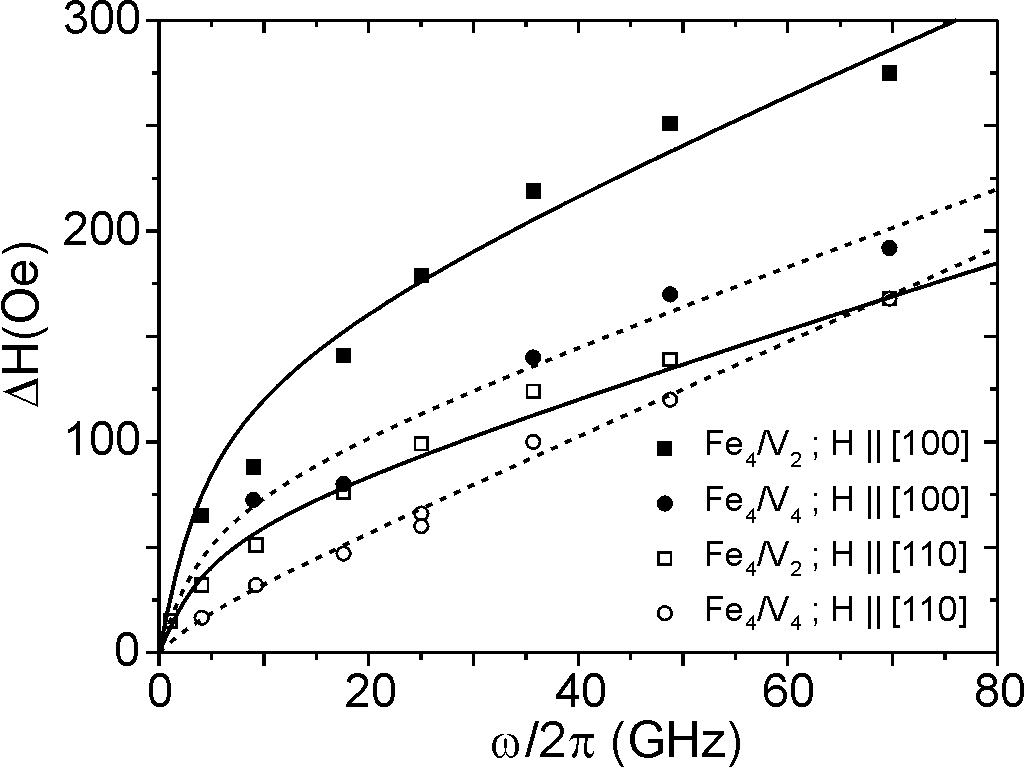
This term can be seen as a ‘viscosity type’ of damping for which the energy stored in the precessing magnetization leaks into the thermal bath. For excitations being proportional to e^ift the Gilbert expression leads necessarily to a linear increase of the damping with the excitation frequency f as indicated schematically by the dashed curve in Fig. 9. As shown for the case of Fe/V multilayers in Fig. 10 FMR can be used to test this linear dependence. The measurements performed within a very large frequency window of 1-70 GHz show a clear curvature, in particular for low frequencies. This deviation from the pure Gilbert-like behavior can be understood upon taking the so-called two-magnon scattering as another relaxation mechanism into account. In this process the uniform mode with wavevector k=0 which is excited couples to degenerate modes having wavevectors k>0. The theoretical dependence on the excitation frequency is plotted as dotted curve in Fig. 9. Taking into account a sum of a Gilbert-like contribution and a two-magnon term (solid line in Fig. 9) one is able to fit the experimental data (solid lines in Fig. 10). This shows the importance of non-Gilbert-like contributions to the overall linewidth. Moreover, one observes different curvatures for different orientations of the external field within the film plane (see Fig. 10). This effect can be directly related to the dispersion relation of the spin waves, since the possible final states with k>0 strongly depend on this dispersion which in turn depends on the external field direction.

Fig. 9

Fig. 10